Statistical Modeling
Below is an exmaple of the type of statistical modeling made possible with the rating system. The dataset that the model below is based in is all FIFA international matches from 1872 to August 17, 2013 (in total 35,872 matches).
 FIFA Internationals
FIFA Internationals
The sport of football has evolved substantially since the first recognized FIFA match between England and Scotland on the 30th of November 1872. Consequently, a regression model based over the entire period that the dataset comprises would be inadvisable. The number of matches per game has varied considerably over time. Below is a chart of goals per match 1872-2013 (the line is a 5 year moving average):


A series of simple regression models that cover a decade (or more) of data would provide a better fit and thus will be used in this example.
 Simple Linear Regression
Simple Linear Regression
A simple linear regression model will suffice to provide a reasonable fit.

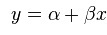
In the equation above, the
y represents what we are trying to model (the amount of goals scored for a given country), the α represents the intercept of the regression, while the β is the value used to predict (the difference between the two country ratings).
 Simple Linear Regression Models
Simple Linear Regression Models
After fitting the data, the following models can be used to model and predict FIFA international matches.
First we model the goals scored for the Favorite (the team with the higher rating). Then we model for the Underdog (the country with the lower rating). Note that for the underdog there is a MIN column. This value is a minimum floor for goals scored for the underdog.
|
FAVORITE |
|
UNDERDOG |
| TIME | Matches | α | β |
|---|
| Pre 1920 | 544 | 1.461 | 0.664 |
| 1920-1945 | 2,022 | 1.580 | 0.667 |
| 1946-1959 | 2,025 | 1.586 | 0.676 |
| 1960-1969 | 2,564 | 1.186 | 0.800 |
| 1970-1979 | 3,705 | 1.009 | 0.773 |
| 1980-1989 | 5,033 | 0.852 | 0.779 |
| 1990-1999 | 6,971 | 0.894 | 0.808 |
| 2000-2009 | 9,440 | 0.867 | 0.822 |
| 2010- | 3,572 | 0.899 | 0.753 |
| | 35,876 | | |
|
|
| TIME | Matches | α | β | MIN |
|---|
| Pre 1920 | 544 | 1.461 | -0.130 | 0.68 |
| 1920-1945 | 2,022 | 1.580 | -0.161 | 0.68 |
| 1946-1959 | 2,025 | 1.586 | -0.154 | 0.47 |
| 1960-1969 | 2,564 | 1.186 | -0.139 | 0.43 |
| 1970-1979 | 3,705 | 1.009 | -0.127 | 0.25 |
| 1980-1989 | 5,033 | 0.852 | -0.168 | 0.23 |
| 1990-1999 | 6,971 | 0.894 | -0.125 | 0.33 |
| 2000-2009 | 9,440 | 0.867 | -0.132 | 0.36 |
| 2010- | 3,572 | 0.899 | -0.124 | 0.33 |
| | 35,876 | | | |
|
 Example
Example
Consider the friendly match between England and Scotland played at Wembley Stadium, London, on 14th of August, 2013. The annual ratings going into the match were England at 100.20 and Scotland 98.35. Empirically it was found that the home field advantage for FIFA matches dictates that the home team increase its rating by 0.27, while the away team decreases its rating by 0.27. This changes the ratings (including home field advantage) to England 100.47, Scotland 98.08, with the rating differential calculated as (100.47 - 98.08 = 2.39). Thus the predictor variable (x) is
2.39
To get the final scores, we now utilize the appropriate simple linear equations. Since this match occurred in 2013 we use the following equations:
FAVORITE
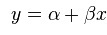 y
y= 0.899 + (.753)* 2.39
y= 0.899 + 1.7997
y= 2.669
England would be expected to score
2.7 goals.
UNDERDOG
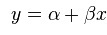 y
y= 0.899 + (-0.124)* 2.39
y= 0.899 -.2964
y= 0.6026
Scotland would be expected to score
0.6 goals.
The model score was: England 2.7 Scotland 0.6
The actual score was: England 3 Scotland 2
 Error
Error
We can use empirical historical data to guage the error of the model. Below is a table detailing the actual goal scoring distributions for those countries that the model predicted 2.7 and 0.6 goals, respectively:
| GOALS: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | TOTAL |
|---|
| 2.70 | 9 | 18 | 29 | 29 | 17 | 5 | 1 | 108 |
| 0.60 | 225 | 110 | 28 | 6 | 1 | 0 | 0 | 370 |
Below is the percent distribution:
| GOALS | 0 | 1 | 2 | 3 | 4 | 5 | 6 | TOTAL |
|---|
| 2.70 | 8.3% | 16.7% | 26.9% | 26.9% | 15.7% | 4.6% | 0.9% | 100.00% |
| 0.60 | 60.8% | 29.7% | 7.6% | 1.6% | 0.3% | 0.0% | 0.0% | 100.00% |
From these empirical distributions we can derive an estimate of the probabilities of all scorelines. Below is the table of all scorelines ranked from most probable to least. The actual 3-2 scoreline should occur approximately 2% of the time. Given the differential in ratings, we would expect an England win 82.04% of the time, a draw 12.53% of the time, and a Scotland win 5.42% of the time.
| England | Scotland | Pct Eng | Pct Sco | PROB | CUM PROB | RESULT |
|---|
| 2 | 0 | 26.85% | 60.81% | 16.329% | 16.329% | ENGLAND WIN |
| 3 | 0 | 26.85% | 60.81% | 16.329% | 32.658% | ENGLAND WIN |
| 1 | 0 | 16.67% | 60.81% | 10.135% | 42.793% | ENGLAND WIN |
| 4 | 0 | 15.74% | 60.81% | 9.572% | 52.365% | ENGLAND WIN |
| 2 | 1 | 26.85% | 29.73% | 7.983% | 60.348% | ENGLAND WIN |
| 3 | 1 | 26.85% | 29.73% | 7.983% | 68.331% | ENGLAND WIN |
| 0 | 0 | 8.33% | 60.81% | 5.068% | 73.398% | DRAW |
| 1 | 1 | 16.67% | 29.73% | 4.955% | 78.353% | DRAW |
| 4 | 1 | 15.74% | 29.73% | 4.680% | 83.033% | ENGLAND WIN |
| 5 | 0 | 4.63% | 60.81% | 2.815% | 85.848% | ENGLAND WIN |
| 0 | 1 | 8.33% | 29.73% | 2.477% | 88.326% | SCOTLAND WIN |
| 2 | 2 | 26.85% | 7.57% | 2.032% | 90.358% | DRAW |
| 3 | 2 | 26.85% | 7.57% | 2.032% | 92.390% | ENGLAND WIN |
| 5 | 1 | 4.63% | 29.73% | 1.376% | 93.766% | ENGLAND WIN |
| 1 | 2 | 16.67% | 7.57% | 1.261% | 95.028% | SCOTLAND WIN |
| 4 | 2 | 15.74% | 7.57% | 1.191% | 96.219% | ENGLAND WIN |
| 0 | 2 | 8.33% | 7.57% | 0.631% | 96.849% | SCOTLAND WIN |
| 6 | 0 | 0.93% | 60.81% | 0.563% | 97.412% | ENGLAND WIN |
| 2 | 3 | 26.85% | 1.62% | 0.435% | 97.848% | SCOTLAND WIN |
| 3 | 3 | 26.85% | 1.62% | 0.435% | 98.283% | DRAW |
| 5 | 2 | 4.63% | 7.57% | 0.350% | 98.634% | ENGLAND WIN |
| 6 | 1 | 0.93% | 29.73% | 0.275% | 98.909% | ENGLAND WIN |
| 1 | 3 | 16.67% | 1.62% | 0.270% | 99.179% | SCOTLAND WIN |
| 4 | 3 | 15.74% | 1.62% | 0.255% | 99.434% | ENGLAND WIN |
| 0 | 3 | 8.33% | 1.62% | 0.135% | 99.570% | SCOTLAND WIN |
| 5 | 3 | 4.63% | 1.62% | 0.075% | 99.645% | ENGLAND WIN |
| 2 | 4 | 26.85% | 0.27% | 0.073% | 99.717% | SCOTLAND WIN |
| 3 | 4 | 26.85% | 0.27% | 0.073% | 99.790% | SCOTLAND WIN |
| 6 | 2 | 0.93% | 7.57% | 0.070% | 99.860% | ENGLAND WIN |
| 1 | 4 | 16.67% | 0.27% | 0.045% | 99.905% | SCOTLAND WIN |
| 4 | 4 | 15.74% | 0.27% | 0.043% | 99.947% | DRAW |
| 0 | 4 | 8.33% | 0.27% | 0.023% | 99.970% | SCOTLAND WIN |
| 6 | 3 | 0.93% | 1.62% | 0.015% | 99.985% | ENGLAND WIN |
| 5 | 4 | 4.63% | 0.27% | 0.013% | 99.997% | ENGLAND WIN |
| 6 | 4 | 0.93% | 0.27% | 0.003% | 100.000% | ENGLAND WIN |
E-mail:
crankshaw_m@bls.gov